{지난 시간}
...
score function에 대해서
SVM의 loss인 hinge loss에 대해서
softmax의 loss인 cross entropy loss에 대해서
규제(regularizaiton)에 대해서
최적화(optimization)에 대해서
경사하강법에 대해서
...
배웠다!

일반적으로 계산하는 방법은 numerical 방법이다.
근데 이건 속도가 느리고 정확하지 않다는 단점이 있다.
그래서 우리는 해석적 방법(분석적 방법)인 analytic 방법을 많이 사용하고
보통 gradient check를 할 때 numerical gradient를 사용한다고 배웠다.

앞에서 배웠던 것을 그림으로 표현하면 이와 같이 된다.
Wx가 곱해져서 들어오고
그 score 값을 function에다가 넣고
거기에 규제를 추가해서
loss가 나오게 되는 것이다.



그리고 여기 AlexNet, Neural Tunring Machine이 있는데
이런 그림과 같은 층을 계속 이어서 이렇게 네트워크를 쌓을 것이다.

지난 시간에 배웠던 gradient를 이제 자세히 볼 것이다.
어떻게 gradient를 이용하여 가중치를 업데이트 시키는지 자세히 배워볼 것이다.
여기서 backpropagaiton을 배울 것이다.
먼저 간단하게 위와 같이 예시가 나왔다고 가정하자.
(x+y) * z 식으로 표현되어 있고
x=-2, y=5, z=-4라고 하자.
그걸 이제 더하고, 곱하면 초록색 값과 같이 -12가 나오게 될 것이다.

근데 우리는 이제 이걸 알아야 한다.
x가 f에 미치는 영향, y가 f에 미치는 영향, z가 f에 미치는 영향
이걸 미분 식으로 표현하면 df/dx, df/dy, df/dz로 표현한다.
그럼 얘를 어떻게 구해야 할까? 바로 미분으로 구하게 된다.
먼저 미분을 구할 때 필요한 식을 몇 개 써보자.
q=x+y의 식에서 dq/dx=1, dq/dy=1이다.
이건 편미분이다.
f=qz에서 df/dq=z, df/dz=q이다.
여기서의 특징을 알아낼 수 있다.
덧셈 연산에서 미분은 1이고, 곱셈 연산에서는 서로의 값을 가지게 된다는 것이다.
즉, qz에서 미분을 하면 z에 대해서 미분을 하면 q가 나옥, q에 대해서 미분을 하면 z가 나오는 것이다.
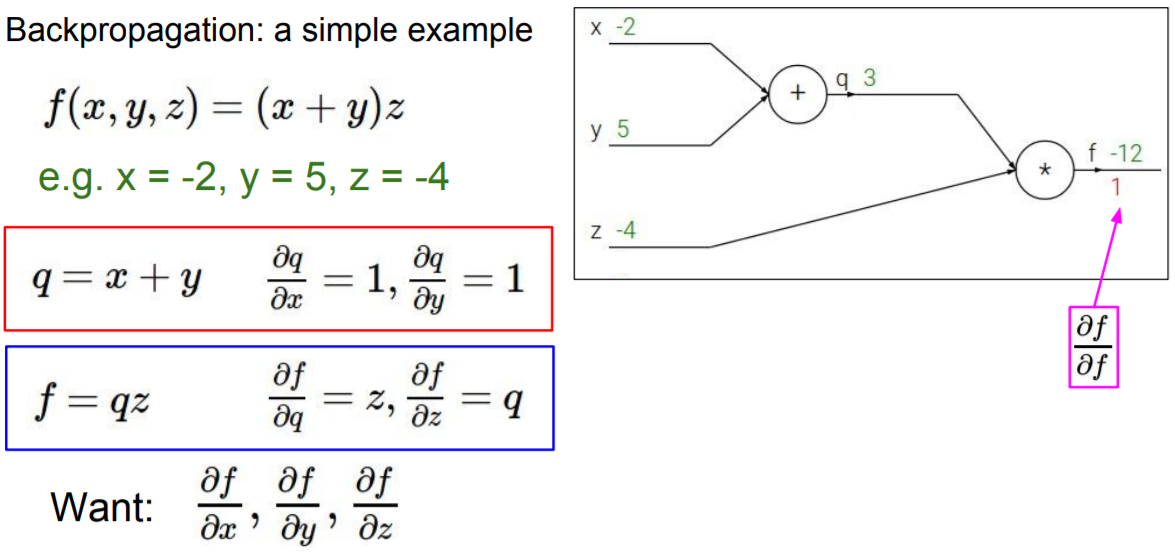
자 이제 계산을 해보도록 하겠다. 앞에서 forward식으로 구했다.
이제 각 값이 최종 f에 영향을 미치는 정도를 파악하기 위해서 gradient를 계산한다.
F가 f에 영향을 미치는 것은 당연히 1일 것이다.

이제 z가 f에 영향을 미치는 정도를 봐보도록 하자.
앞에서 식으로 구해놓은 것을 가져오면 된다.
바로 q값이다.
즉, 3이다.


q가 f에 영향을 미치는 것도 마찬가지이다.
앞에서 구했듯이 z가 될 것이고 z값인 -4가 될 것이다.

자 이제 문제는 y가 f에 미치는 영향 및 x가 f에 미치는 영향 값을 구해야 한다.
여기서 바로 direct로 구할 수 없으니, chain rule을 적용시켜야 한다.
Chain Rule은 미분에서 사용되는 방법이다.
만약, x가 f에 대해서 영향을 미치는 값을 알고 싶으면 x -> q -> f 이므로
x가 q에 미치는 영향 * q가 f에 미치는 영향
이런 식으로 구하면 된다.
아까 간단한 미분식으로 구한 q가 f에 미치는 영향과
이미 구해놓은 x+y의 미분값인 1
이 두 가지를 local gradient라고 부른다.
이 local gradient는 forward passing을 하면서 그냥 구해버릴 수 있기 때문에
미리 값을 가지고 있다.
이제 y가 q에 미치는 영향만 알면 되는데 이미 그 값을 알고 있다.
바로 1이다.
그래서 1*q를 하니 -4가 된다.

x도 마찬가지이다.
그래서 qz나 x+y 같은 미리 구할 수 있는 미분 값을 local gradient라고 한다.
이 local 값과 앞에서 넘어온 gradient를 global gradient라고 하는데
이 값을 곱해서 gradient를 계산한다.

그럼 여기서 끝인가? 위 예에서는 위의 노드로 끝이지만 실제로는 앞에서 더 많은 node들이 있을 것이다.
그래서 여기서 구한 gradient를 다시 뒤로 보내고 그럼 global gradient값이 될 것이다.
그리고 뒤에 있는 local gradient와 이 받은 global gradient를 곱해서 다시 gradient값을 구하고...
이러한 과정을 반복한다.
이렇게 적절한 gradient를 찾아가는 것이다.
심화된 내용으로 시그모이드(sigmoid)를 해보자.
시그모이드도 미리 계산하기 편하도록 local gradient의 식을 써보면 아래와 같이 4가지가 나올 것이다.
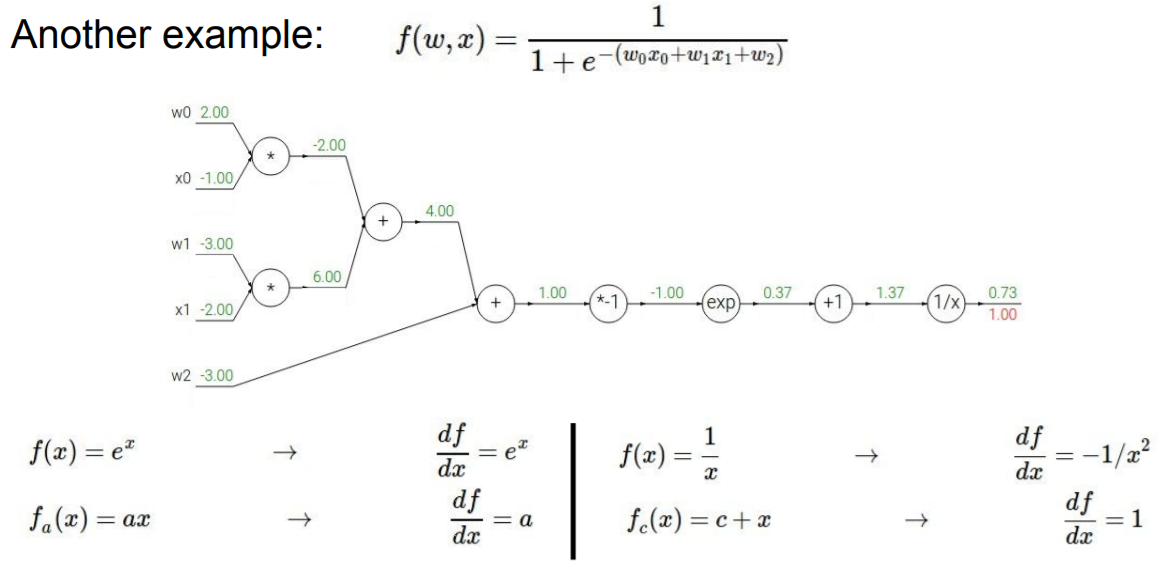
맨처음 gradient는 당연히 1이다. 그리고 다음 과정을 해보도록 하자.

1.37쪽 기준에서는 global gradient는 1이다.
그리고 1/x이니까 local gradient는 -1/x^2가 된다.
즉, -1/1.37^2와 1을 곱하면 되는 것이므로 gradient는 -0.53이 나오게 된다.
다음 과정으로 넘어가보자.

0.37 기준에서는 global이 -0.53이 된다. 근데 여기서 local은 1이므로
1 * -0.53을 하면 -0.53이 된다.

EXP를 하는 부분에서 보면 global은 -0.53이고 local은 e^x 값 즉, e^-1이 되므로
gradient값은 -0.20이 나오게 된다.

그리고 그 다음은 0.2가 나오게 된다.
이제 덧셈 연산을 거치면 다시 0.2가 나오게 되고 아래 그림들처럼 구해주면 된다.



여기서 sigmoid gate라는 부분이 있는데
이 부분을 우리는 앞에서 하나하나 구했지만 굳이 그럴 필요가 없다.
위의 미분 과정을 거치면 시그모이드 식은 맨 아래처럼 나오게 된다.
이를 일반화 하게 되면
(1-sigmoid) * sigmoid 로 표현할 수 있다.
즉, sigmoid 게이트가 들어가기전 gradient는 sigmoid값인 0.73을 기준으로
(1-0.73) * 0.73으로 구할 수 있다는 것이다.
굳이 복잡하게 하나하나 계산하지 않고도 바로 구할 수 있다는 것이다.

여기서 또 gradient의 특성을 알 수 있다.
바로 add, mul 등의 gate에 대한 특징이다.
add는 local이 1이라서 gradient가 global값 그대로 나온다.
즉, add gate는 gradient를 그대로 전해주는 역할을 하게 된다.
그래서 distributor라고 불린다.
max gate는 큰 값에게 gradient를 그대로 전하고
작은 값은 0으로 그냥 만들어서 보내는 것이다.
mul gate는 서로의 값을 교환한다.
qz라고 하면 q는 z값을 가지게 되고 z는 q의 값의 가지게 된다.
즉, 스위칭 역할을 한다.
그래서 mul gate는 switcher라고 불린다.

근데 만약 앞에서 온 gradient가 1가 아니라 여러 개면 어떻게 될까?
위 그림처럼 말이다.
그러면 그냥 복수의 gradient를 더해준다.

근데 우리는 이게 하나의 값이 아니라 다변수일 확률이 높다.
보통 딥러닝이 그렇다.
그럴땐 자코비안 행렬 방식으로 되게 된다.
자코비안 행렬은 다변수 함수일때의 미분값들의 행렬이다.

그래서 input이 이제 d차원의 벡터가 들어가게 된다.
그리고 output도 d차원의 output이 된다.
그럼 jacobian matrix의 크기는 어떻게 될까?
input도 4096이고 output도 4096이니까
4096 x 4096이 될 것이다.

근데 여기에 minibatch를 추가하게 되면
예를 들어 100개씩이면 100을 곱해야한다.
그래서 409600 x 409600이 된다.
이는 매우 거대하다. 근데 실제로는 이 거대한 자코비안 행렬을 계산하지 않는다.
여기서 어떤 구조가 보이냐면 이거는 요소별로 보기때문에 입력의 각 요소 즉 첫번째 차원은 오직 출력의 해당 요소에만 영향을 주기 때문이다. 그렇기 때문에 자코비안 행렬은 대각행렬이 된다! 그래서 실제로 이 전체 자코비안 행렬을 작성하고 공식화할 필요가 없다는 것이다. 우리는 출력에 대한 x의 영향과 이 값을 사용한다~ 이런식으로만 알면 된다. 그리고 계산되어 나온 gradient를 채워 넣는 것이다. 그냥 그렇구나~ 하고 넘어가면 될 것 같다.
이제 더 구체적으로 봐보도록 하자.

위 예시를 보면 규제값을 넣어서 x에 의해 곱해진 W의 L2처럼 만든다.
이 경우 x를 n차원이라고 하고 W는 n*n이라고 하자.

그림으로 표현하면 위와 같다.

그리고 앞에서 한 것처럼 q=wx이고, w와 x가 각 값이 저렇게 된다고 보자.
이제 행렬곱을 하면 아래 식처럼 되고 우리는 L2 정규화를 했으니 제곱을 하게 된다.
계산해보면 위와 같다.
위에 0.22가 어떻게 나오게 되는 것일까?
0.1 * 0.2 + 0.5 * 0.4 를 해서 나오게 된다.
0.26은 -0.3과 0.8 기준이다.
그리고 0.22와 0.26이 행렬곱에 의해서 나오게 된다. 이 값들을 이제 각각 제곱을 한다.
0.22를 제곱하면 0.048이고,
0.26을 제곱하면 0.067이 나온다.
이 둘을 더하면 0.116이 나오게 된다.
이제 gradient를 구해보자!

맨 처음은 역시나 1이다.
그리고 qi가 df에 미치는 영향은 2qi 이므로 (qi^2 미분값) 우리는 2q값을 취하면 된다.
그래서 local이 2q이고 global이 1이므로 0.44, 0.52값이 나오게 된다.

그리고 다음을 구해보도록 하자.
dWi,j일 때 dqk를 구해야한다. 즉, w가 q에 미치는 영향을 구하는 것이다. 그리고 1=k=ixj가 있는데 이것은 k가 i일때 1이라는 것이다. 그리고 아닌 것은 0으로 두는데 왜 이렇게 두냐면 행렬에서 값을 계산할 때 각 행의 계산 시에 다른 행은 관여하면 안되기 때문이다. 참고로 i는 행, j는 열이다.
그래서 이 식에 대해서 미분값을 구하게 되면 앞 페이지처럼 나오게 된다.
시그마k 옆에 df/dqk는 k일 때 q가 f에 미치는 영향 * w가 q에 미치는 영향이다.
즉, 우리가 앞서 보았던 chain rule이다. 그 chain rule이 다차원을 만나면서 복잡해졌을 뿐이지 원리는 같다.
그래서 결국은 2qixj가 된다.
0.088이 왜 나왔을까?
바로 앞에서 온 gradient인 0.44 * 0.2을 했기에 0.088이 나온다.
왜냐하면 이제 2x2 행렬이 나와야 한다. 그래서 x를 전치(T)시킨다.
그래서 2x1 행렬이었던 x가 1x2로 되고 앞에서 온 행렬은 2x1 이므로 2x1 행렬 곱하기 1x2 행렬이니까 2x2 행렬이 나오게 된다. 그렇게 다른 것도 곱해줘서 구해주면 된다. 마찬가지로 다른 것도 이렇게 구하면 된다.
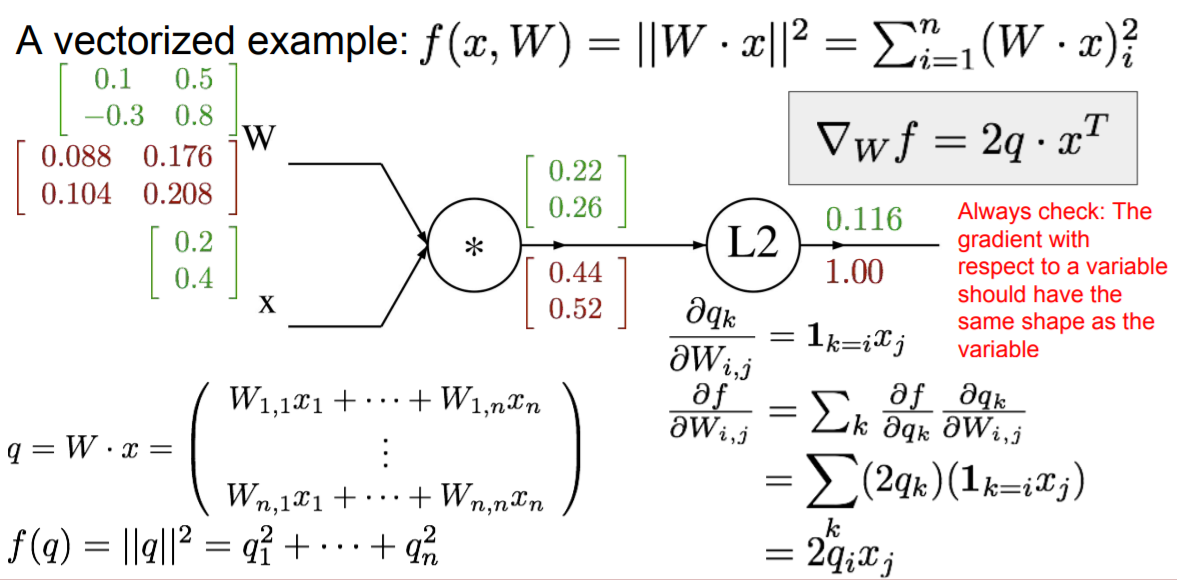
위 식은 우리가 유도한 식을 벡터화된 형식으로 작성한 것이다.
여기서 빨간색으로 중요한 것을 강조했는데 중요한 것은 변수에 대해 gradient를 항상 체크하는 것이다.
이것들은 항상 변수와 같은 shape을 가지고 있다. 무슨말이냐 하면 gradient가 무엇인지 계산을 했으면 이 결과가 변수의 shape과 동일한가?를 체크해야 한다. 이거를 체크하지 않고 그냥 하면 에러가 나올 수 있다. 변수와 같은 shape을 꼭 갖고 있어야 한다.
아래 값에 대한 gradient를 마저 구해보자.
dqk/dxi이다.

x가 q에 미치는 영향이다. 이건 Wk,i이다.
이걸 더 자세한 식으로 계산하면
시그모이드 k df/dqk * dqk/dxi가 된다.
앞에서 했던 chain rule을 적용한 것이다.
마찬가지로 이번에는 w가 전치가 된다.
w가 전치가 되면 첫번째 행은 [0.1, -0.3]이 되고 두번째 행은 [0.5, 0.8]이 된다.
그래서 0.1 * 0.44 + -0.3 * 0.52를 하게 되면 -0.112가 나오게 된다.
0.636도 마찬가지로 구하면 된다.



위는 코드화 했을 때 이렇게 된다는 것이다.
곱셈에 대한 클래스는 forward시에는 그냥 곱하지만 backward시에는 x일때는 y값, y일때는 x값을 구한다.
여기선 스칼라니까 전치가 적용되지 않고 그냥 구하면 된다. 벡터면 당연히 전치가 들어가게 된다.
파이썬 numpy에선 .T 연산자로 간단하게 전치가 가능하다.

간단한 요약이다.
이제 뉴럴 네트워크에 대해서 알아보자!

우리는 과거에 이렇게 단순한 linear한 score를 알아보았다.
f = Wx 이다.
근데 이제는 W2max(0, W1x)와 같이 된다.
ReLU에서 이렇게 사용한다.
처음에 3072개의 x가 들어오면 w1과 곱해져서 중간인 hidden node에 들어갔다가
나와서 다시 10개의 출력값(CIFAR-10)으로 나오게 된다.
즉, 중간에 히든 레이어가 하나 더 생기게 되었다. 이는 과거에 그냥 하나의 분류기로 판단했던 것과 다르다.
이 그림은 우리가 과거에 봤던 하나의 분류기로 했던 것이다. 말 머리가 2개로 보이는 등 잘 분류가 되지 않았다.
근데 이제는 이야기가 달라진다. hidden node가 100개면 우리는 서로 다른 100개의 분류기를 가지고 있는 것이다.

만약, 3-layer면 이렇게 될 것이다.

이를 numpy로 짜보면 이런 식으로 나오게 된다.
exp는 e^승 연산이고 dot은 행렬곱 연산이다.


여태 배워왔던 것과 뇌속의 뉴런과 굉장히 비슷하다.
활성화 함수는 우리가 전에 배웠던 시그모이드 함수와 같은 것이 된다.

그리고 우리는 여태 activation functions를 sigmoid로 계속 봐왔지만
실제로는 다양한 활성화 함수가 존재한다.

보통은 ReLU를 많이 사용한다.
그리고 우리가 앞에서 봤던 2-layer나 3-layer는 서로 fully하게 connect되어 있다.
그래서 fully connected라고 한다.
줄임말로는 fc라고 많이 불린다.



오늘은 여기까지 :)
(참고자료)
leechamin.tistory.com/search/cs231n
참신러닝(Fresh - Learning)
이차민의 iOS/ML/DL 공부 블로그 Computer Vision과 iOS개발에 대한 전반적인 공부를 합니다. "Be The First Penguin"
leechamin.tistory.com
꿈 많은 사람의 이야기
안녕하세요. 이수진이라고 합니다. 이 블로그는 AI(인공지능), Data Science(데이터 사이언스), Machine Learning, Deep Learning 등의 IT를 주제로 운영하고 있는 블로그입니다.
lsjsj92.tistory.com
taeyoung96.github.io/categories/CS231n/
CS231n Summary
한 발자국씩 앞으로 나아가자
taeyoung96.github.io
'ML & DL > CS231n (Stanford Univ.)' 카테고리의 다른 글
| [CS231n] Lecture 6 | Training Neural Networks I (0) | 2020.11.28 |
|---|---|
| [CS231n] Lecture 5 | Convolutional Neural Networks (0) | 2020.11.14 |
| [CS231n] Lecture 3 | Loss Functions and Optimization (0) | 2020.10.24 |
| [CS231n] Lecture 2 | Image Classification (0) | 2020.10.14 |
| [CS231n] Lecture 1 | Introduction to Convolutional Neural Networks for Visual Recognition (0) | 2020.10.10 |




댓글